Performance analysis for binary classification

This function performs an analysis sensitivity and specificity to asses the performance of a binary classification test. For further reading the studies by Brenner and Gefeller 1997, James 2013 by Kuhn 2008 are a good starting point.

performeR(sample, reference)

Arguments

sample

is a vector with logical decisions (0, 1) of the test system.
reference

is a vector with logical decisions (0, 1) of the reference system.

Details

TP, true positive; FP, false positive; TN, true negative; FN, false negative

Sensitivity - TPR, true positive rate TPR = TP / (TP + FN)

Specificity - SPC, true negative rate SPC = TN / (TN + FP)

Precision - PPV, positive predictive value PPV = TP / (TP + FP)

Negative predictive value - NPV NPV = TN / (TN + FN)

Fall-out, FPR, false positive rate FPR = FP / (FP + TN) = 1 - SPC

False negative rate - FNR FNR = FN / (TN + FN) = 1 - TPR

False discovery rate - FDR FDR = FP / (TP + FP) = 1 - PPV

Accuracy - ACC ACC = (TP + TN) / (TP + FP + FN + TN)

F1 score F1 = 2TP / (2TP + FP + FN)

Likelihood ratio positive - LRp LRp = TPR/(1-SPC)

Matthews correlation coefficient (MCC) MCC = (TP*TN - FP*FN) / sqrt(TN + FP) * sqrt(TN+FN) )

Cohen's kappa (binary classification) kappa=(p0-pc)/(1-p0)

r (reference) is the trusted label and s (sample) is the predicted value

r=1r=0
s=1ab
s=0cd

$$n = a + b + c + d$$

pc=((a+b)/n)((a+c)/n)+((c+d)/n)((b+d)/n)

po=(a+d)/n

References

H. Brenner, O. Gefeller, others, Variation of sensitivity, specificity, likelihood ratios and predictive values with disease prevalence, Statistics in Medicine. 16 (1997) 981--991.

M. Kuhn, Building Predictive Models in R Using the caret Package, Journal of Statistical Software. 28 (2008). doi:10.18637/jss.v028.i05.

G. James, D. Witten, T. Hastie, R. Tibshirani, An Introduction to Statistical Learning, Springer New York, New York, NY, (2013). doi:10.1007/978-1-4614-7138-7.

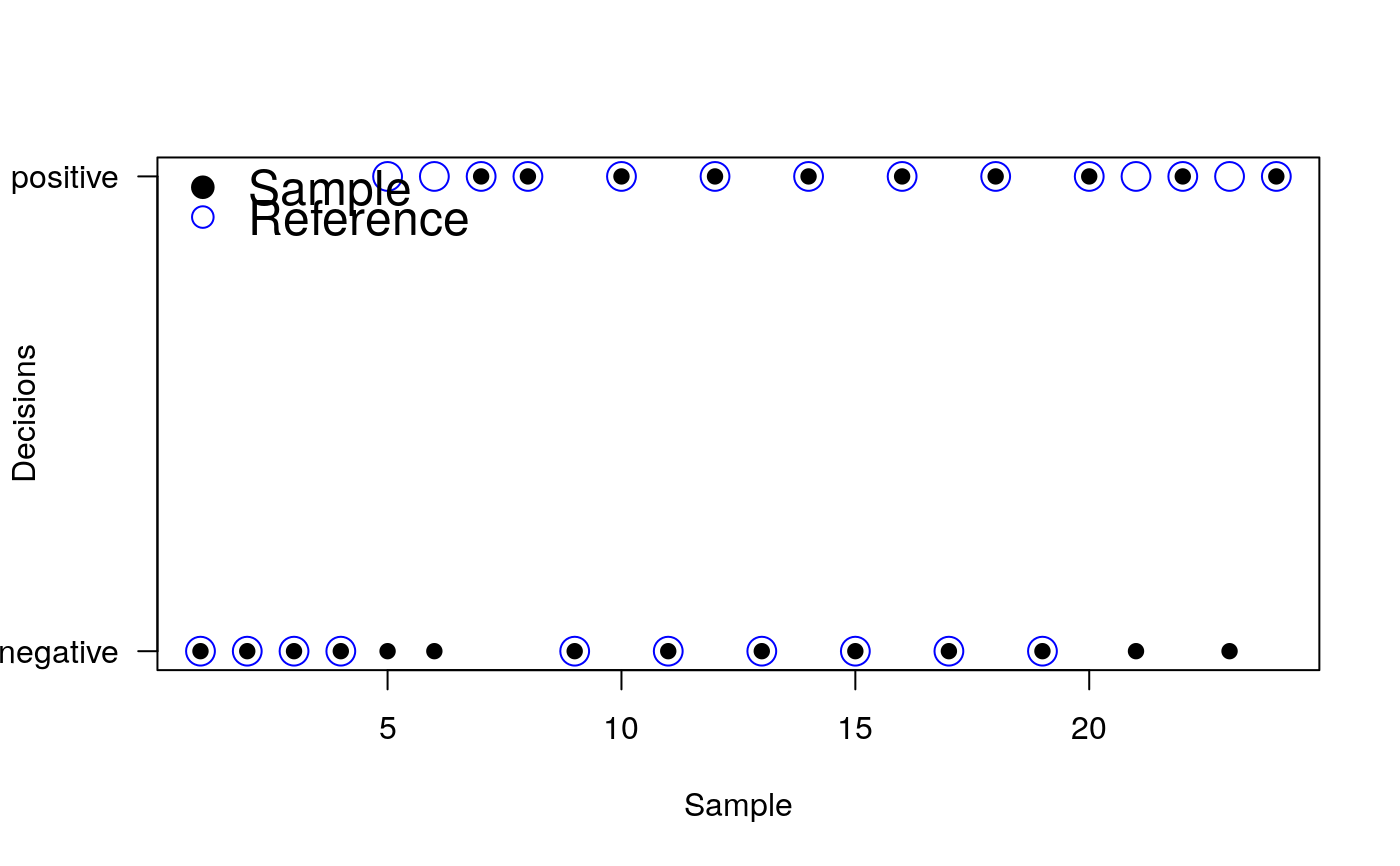
Examples

# Produce some arbitrary binary decisions data
# test_data is the new test or method that should be analyzed
# reference_data is the reference data set that should be analyzed
test_data <- c(0,0,0,0,0,0,1,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1)
reference_data <- c(0,0,0,0,1,1,1,1,0,1,0,1,0,1,0,1,0,1,0,1,1,1,1,1)

# Plot the data of the decisions
plot(1:length(test_data), test_data, xlab="Sample", ylab="Decisions",
     yaxt="n", pch=19)
axis(2, at=c(0,1), labels=c("negative", "positive"), las=2)
points(1:length(reference_data), reference_data, pch=1, cex=2, col="blue")
legend("topleft", c("Sample", "Reference"), pch=c(19,1),
        cex=c(1.5,1.5), bty="n", col=c("black","blue"))

# Do the statistical analysis with the performeR function
performeR(sample=test_data, reference=reference_data)
#>         TPR SPC PPV       NPV FPR       FNR FDR       ACC        F1       MCC
#> 1 0.7142857   1   1 0.7142857   0 0.2857143   0 0.8333333 0.8333333 0.7142857
#>   LRp     kappa TP TN FP FN counts
#> 1 Inf 0.6756757 10 10  0  4     24